Understand the basics of translational and rotational dynamics

Let's talk about the dynamics which we call motions as well. We know that there are two types of dynamics, one is translational dynamics and other is rotational dynamics. Sometime a motion is only linear which we call translation. So in translation motion of a body will move from one point to another point exactly in a straight line and there will be no curvature, while in rotational motion a body will be moving in a circular motion or spinning and it will have no linear motion. Mostly, we are having the dynamics or the motion of a body as a combination of translational and rotational.

Now, in order to understand the translational and rotational dynamics, first we will have to understand some terminologies and we call the first thing as the physical quantities.

The physical quantities are for example displacement, velocity, acceleration, force etc. Some of the physical quantities are scalars and some are vectors. Now in scalar, we only have number, we only have magnitude while in vectors we are having with this magnitude a direction as well.

We cannot call vectors as horizontal vector or vertical vectors, in order to define them, we define a coordinate system. A vector can also have an inclination, which is called slope of that vector. Vectors can have zero slope or it can have undefined or infinite slope as well.

If suppose a vector is only along y-axis, so I can resolve it into components, the horizontal component and the vertical component.

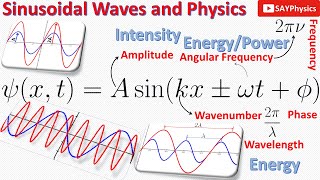
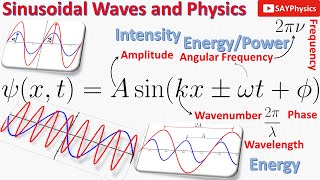
Now let's define some ratios, if we divide the ratio of the \(x\) with \(r\) means the base divided by the hypotenuse, we will call this one as $$ \frac { x }{ r } =\cos { \theta } $$Similarly, the ratio of the perpendicular com ponent with the hypotenuse is $$ \frac { y }{ r } =\sin { \theta } $$These two quantities will actually give us the inclination of a vector. We can write these as $$ x=r\cos { \theta } $$ $$ y=r\sin { \theta } $$ Now we are coming back to our translational and rotational dynamics. The very first thing in Physics that we discuss is called displacement which is denoted by \(x\). It is actually the distance from one point to another point in exactly a straight line or the sharpest distance between two points is called displacement and it's a vector quantity because in a straight line it will have one direction only. We are having its rotational counterpart which we call angular displacement which is represented by \(\theta \). We want to establish a relation between \(x\) and \(\theta \), $$ x\propto \theta $$ But what will be the constant of proportionality? Let's consider a very small displacement, When $$ \theta << d \theta $$ The perpendicular distance was $$ y=r\sin { \theta } $$ $$ dy=r\sin { d\theta } $$ $$ dy=rd\theta $$ Now I can integrate both sides $$ \int _{ 0 }^{ s }{ dy } =\int _{ 0 }^{ 2\pi }{ rd\theta } $$ Here \(y\) is running from zero to any distance, say \(S\) $$ S=2\pi r $$ So I can say that the distance \(S\) which is the linear distance is equal to \(2 \pi r\). This \(2 \pi \) is actually the angle so can write that $$ S=r\theta $$ The linear and angular displacement is related by the radius which we will call moment arm later. The S is called the circumference of the circle.