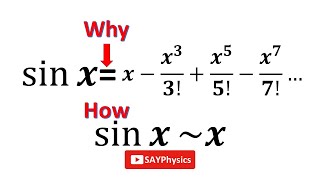Conceptual Physics: Basics of sinusoidal waves and its properties I

In this lecture we will talk about the sinusoidal waves their importance in physics. We will discuss the very general equation of these periodic waves and the different parameters used in these waves. We will discuss those parameters in their relation to the physical quantities.

What are sinusoidal waves? There are many definitions of a wave. A wave is actually a disturbance in a medium that carries energy without a moment of particles we can also define it is a wave is a disturbance of one or more fields such that the field values oscillate repeatedly about a stable equilibrium value.

This is a wave equation $$ \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } ={ v }^{ 2 }\frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } $$ Or $$ \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } ={ c }^{ 2 }\frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } $$ where c is the speed of light.

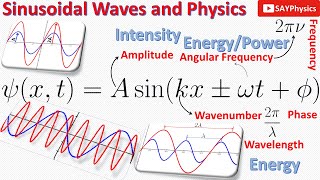
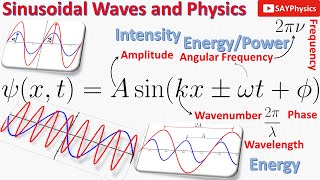
When we come to electromagnetic waves the solution of this equation is $$ \Psi \left( x,t \right) =A\sin { \left( kx\pm \omega t+\varphi \right) } $$ The solution can also be written is a cos means sine is replaced with cos and both are actually sinusoidal varying periodic functions you know the only difference between sine and cosine is actually \(\pi / 2\) radians phase-shift.

So let's discuss this relation
A is actually the amplitude
k is the wave number which is related to the wavelength by \(2 \pi / \lambda \)
\( \lambda \) being the wavelength of the wave
\( \omega \) is the angular frequency
while \( \varphi \) is the phase of the wave.

So, all information is included in this equation which we will discuss one by one.

The very conceptual thing that we will have to keep in mind that all the motions depicted here are actually the simple harmonic motions. If I consider a particle moving in a circle then it equivalent to a particle moving like a sine wave or a particle going up and down means attached to a spring, the equation of them is the same which is the simple harmonic motion equation so all these motions are actually the different representations of the motion while they are the same.

Now the big question here is what happens when two are more than two waves same waves but having different amplitudes then which property of the wave is affected? So the answer is intensity because intensity is directly proportional to the square of the amplitude more the amplitude of a wave more will be the intensity of the wave.

Now we will have to understand the intensity $$ P = E/t $$ $$ I = P/A $$ This implies that $$ I = E/AT $$ And $$ E={ E }_{ 0 }\cos { \omega t } $$ here \(E_0\) is the permittivity of free space and c is the speed of light .

The question is when the intensity of a wave is change? Does it change its energy the straightforward? The answer is intensity is not only depending on energy but also on the perpendicular area. Let me explain this thing by explaining the photoelectric effect in which we know that when we shine a light of certain energy on a metal surface then the electrons, on the surface the metal surface electrons absorb that energy if the energy of the photon is more equal or more than the surface binding energy of this electron. Then this electron will be ejected out of the metal surface. Intensity is actually the number of photons. Einstein actually said that one photon will interact with one electron only.

If we increase the number of sources then we will increase the number of photons and this increase in number of photon will cause more electrons to get out of the metal surface so here the individual energy of the photon has been changed by changing the source so we say that when intensity is increased. Although the total energy is increased because the total energy is the sum of the energy of all photons.